欧拉!天才高斯——19世纪最伟大的数学家,近代数学的奠基者

文章插图
卡尔·弗里德里希·高斯(1777~1855)是一个神童。19岁差一个月的他作出了一项非凡的发现。2000多年以来,人们知道如何用直尺和圆规作等边三角形和正五边形(还有其他的正多边形,其边数是2、3、5的倍数),但不知道如何作出边数为素数的正多边形。高斯证明,正七边形也能用直尺和圆规作出。

文章插图
- 高斯日记
我们可用图示的方法解方程
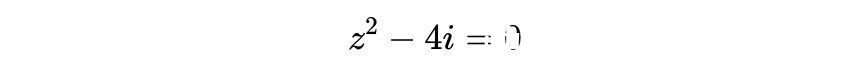
文章插图
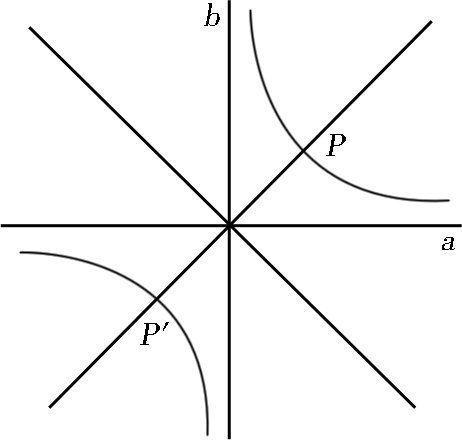
【 欧拉!天才高斯——19世纪最伟大的数学家,近代数学的奠基者】证明存在一个复数值z=a+bi满足这个方程。用a+bi取代z,并分开方程中的实数部分和虚数部分,我们就得到a^2-b^2=0和ab-2=0。把a和b解释为变量,并在同一坐标系中画出这些函数,一个坐标轴代表实数部分a,另一个坐标轴代表虚数部分b,我们就有了两条曲线;一条由直线a+b=0和a-b=0构成,另一条由等轴双曲线ab=+2构成。
文章插图
很显然,这两条曲线有一个交点P在第一象限。我们应该特别注意,第一条曲线的一条分支沿着θ=1π/4和θ=3π/4的方向离开原点;第二条曲线的一条分支渐近地向着θ=0π/4和θ=2π/4的方向移动;交点在最后两个方向θ=0和θ=π/2之间。这个交点的a和b的坐标是方程z^2-4i=0的一个解的实数部分和虚数部分。假如我们最初的多项式方程是三次而不是二次,则一条曲线的一根分支就会趋近于θ=1π/6和θ=3π/6的方向,另一条曲线就会趋近于θ=0π/6和θ=2π/6的方向。在每一种情况下这些分支都是连续的,因此,它们一定要相交于θ=0至θ=π/3之间的某个地方。
对于一个n次方程来说,一条曲线的一根分支有渐近方向θ=1π/2n和θ=3π/2n,而另一条曲线的分支有渐近方向θ=0π/2n和θ=2π/2n。这些分支必定相交于从θ=0至θ=π/n之间,这个交点的a和b的坐标,就是满足这个方程的复数的实数部分和虚数部分。因此我们看到,不管一个多项式方程的次数是几,它必定至少有一个复数根。我们会注意到,高斯依靠这些曲线的图示来证明它们相交。承认这个结果,多项式方程可以分解为一次或二次实因子也就得到了证明。
数论高斯在他还是哥廷根大学的一名学生的时候,就开始撰写一部重要的数论著作——《算术研究》,是数学文献中的伟大经典之一,在他的博士论文通过两年之后出版。此书由7个部分组成。前4个部分本质上是对18世纪数论的浓缩重构。讨论的基本原则是同余和剩余类的概念。第5部分致力于二元二次型理论,特别是形如
的方程的解的问题;这一部分所发展出来的技术,成了后来一代代数论学家所做的大量工作的基础。第6部分由各种不同的应用所组成。最后一部分起初吸引了最多的关注,处理的是次数为素数的割圆方程的解。
- 我们的天才儿子|《我们的天才儿子》常来的浙图,浙图找出了他的翻译十部作品
- 老人|“天才儿子”已出院回家!父亲最新回应:这些心里话以前不敢讲,现在他接受了,我的心也放下了......
- 我们的天才儿子|《我们的天才儿子》全网刷屏,父亲最新回应
- 金晓宇|“天才儿子”刷屏!回应来了
- 躁郁症@《我们的天才儿子》全网刷屏,父亲回应:小宇已回家,正在翻译新书
- 金晓宇|“住在精神病院的天才儿子”刷屏,网友们泪流满面,父亲最新回应
- 小宇|《我们的天才儿子》全网刷屏,父亲回应:小宇已回家,正在翻译新书
- 电话|杭州男子从殡仪馆打来电话:能不能写写我们的天才儿子
- 金晓宇|住精神病院成天才,这篇文章全网刷屏,父亲回应
- 金晓宇|“住在精神病院的天才儿子”刷屏,网友们泪流满面
