换个说法吧 , 我们看一个篮球就是曲面球体 , 而篮球上的一只蚂蚁看来篮球就是一个平面 , 同理 , 蚂蚁看到的一段直线在我们看来就是一段弧线 。
其实欧几里得说的直线应该叫做测地线 , 几何学的含义就是测量大地的学问 , 这就是说几何学的基础就在测量大地上 , 测地线就是在地面上一点到另一点的距离 , 我们知道我们居住的大地是球形的 , 这样看来的话 , 欧几里得所谓的直线也是曲线 。
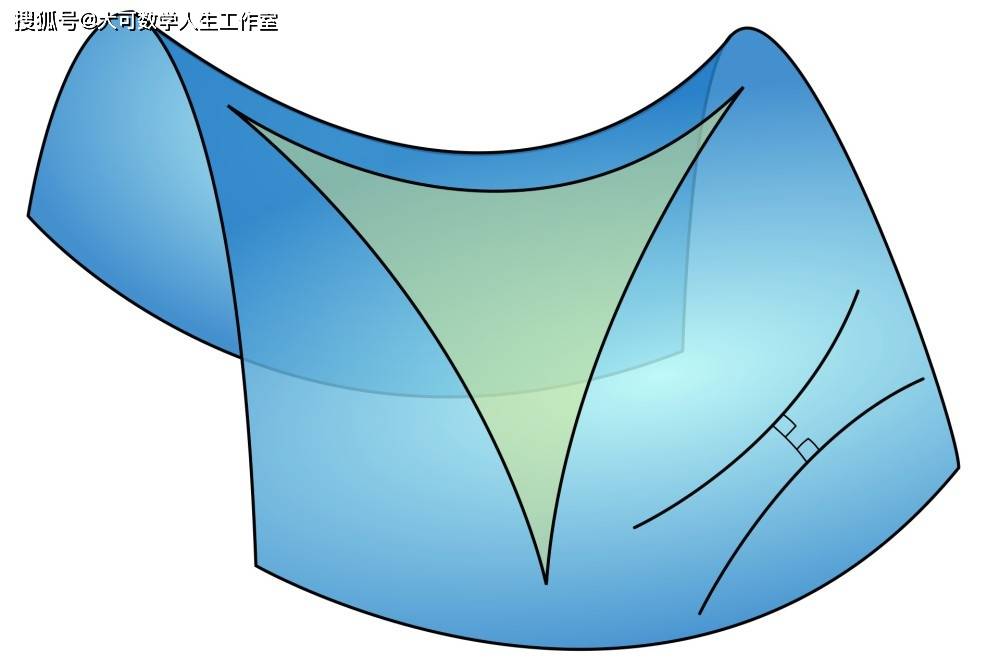
依照高斯的观点 , 罗巴切夫斯基的非欧几何就是在曲面上的几何学 , 我们还是来看一张图吧 。
文章图片
这就是罗巴切夫斯基的非欧几何 , 这可以看出来 , 曲面上三角形的内角和小于180° , 通过直线外一点的平行线也不止一条 , 因为这是一个双曲曲面上 , 因此罗巴切夫斯基的非欧几何也叫做双曲几何 。
高斯不但在理论上阐述了这个问题 , 他还做了实验 。
在1818年到1826年期间 , 高斯主导了汉诺威公国的大地测量工作 , 他曾经测量三个山峰组成的三角形的内角和 , 在高斯看来 , 只要三角形足够大 , 那么就接近曲面 , 只要就可以找到三角形内角和不等于180°的证据 , 可由于当时测量工具的精度不够 , 他并没有得到这个结论 , 这也使得他更不能轻易发表证据的看法了 。
不管怎么说 , 罗巴切夫斯基已经拿到了非欧几何的首创权 , 毕竟他遇到的是高斯而不是牛顿 , 在几何上 , 要说欧几里得就好像托勒密一样 , 那么罗巴切夫斯基就是当之无愧的哥白尼 , 不过也仅仅是哥白尼 。
罗巴切夫斯基推翻了欧几里得 , 就像哥白尼用日心说推翻了托勒密的地心说一样 , 可是日心说并不是最终的真理 , 之后还有伽利略和牛顿 , 罗巴切夫斯基也并不是终点 。
那么由谁来开启新的征程呢?
4.黎曼出世
1826年 , 高斯还在汉诺威公国的大地上忙碌的时候 , 一个婴儿降生在这片土地上 , 他就是命中注定要接过高斯旗帜的黎曼 。

文章图片
在跨入大学前 , 黎曼并没有感受到命运的感召 , 他以一个神学系学生的身份走进了哥廷根大学 , 但命运的力量是不可抗拒的 , 黎曼偶尔听了一场年近古稀的高斯的数学讲座 , 就是这场讲座 , 让黎曼闯进了数学王国 。
获得博士学位后 , 黎曼需要做一个演讲来获得教职 , 他准备了三个题目 , 可到底讲哪个有点难以取舍 , 他去向高斯请教 , 高斯一眼就相中了几何基础 。
对于这个题目 , 黎曼仅仅准备了两个月 , 他自己也并没有多少把握 , 可是既然都相中了 , 那么就一定有他的道理 。
黎曼的演讲就是《论作为几何基础的假设》 , 他的演讲并没有语惊四座 , 据说只有高斯才听懂了他在说什么 , 不过已经足以让所有人大吃一惊 , 黎曼说根本就没有平行线 。
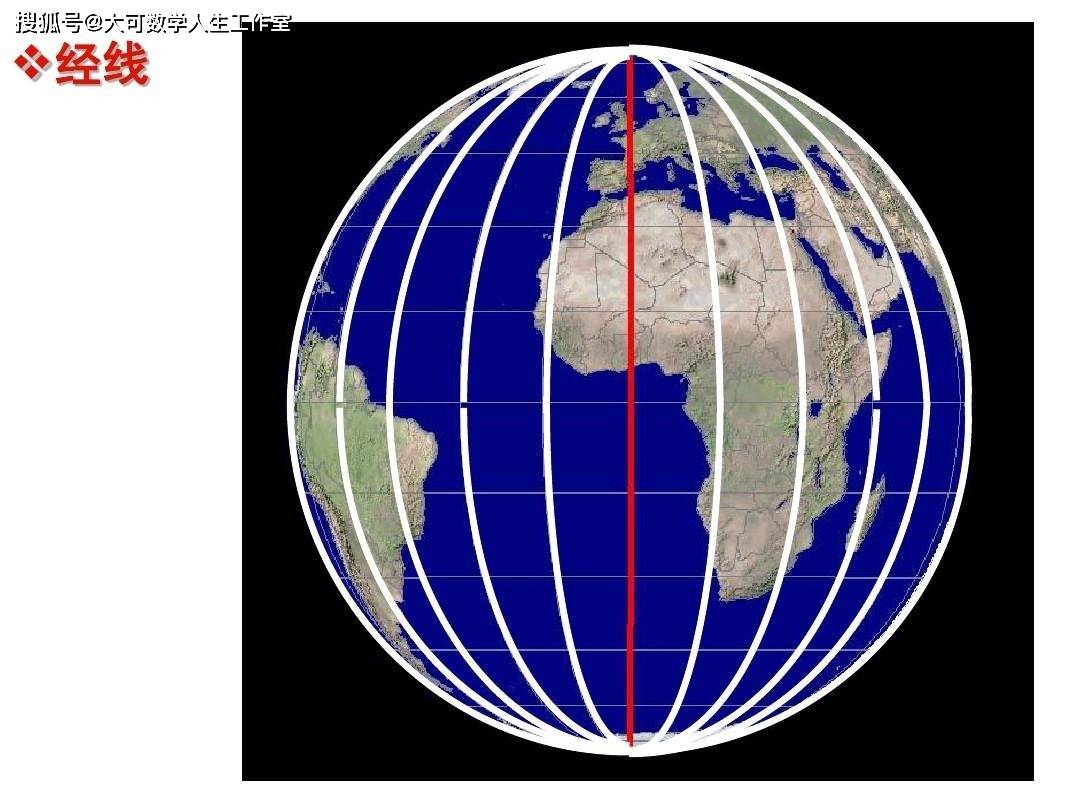
还是用球来打个比方吧 。 这次用地球 。
文章图片
在地球上我们看来经线都是平行的 , 可经线最终都要交汇于南北极 , 这哪里还有什么平行线呢?可是经线不是直线呀 , 谁说经线不是直线呀 , 欧几里得的直线就是测地线 , 经线本来就是测地线呀 , 要是我们穿过地球做一条直线呢 , 那你怎么知道宇宙空间是什么样的呀 , 没准也是个球呢 。
在说黎曼的理论之前 , 还是先来看一下高斯的想法 , 毕竟只有他听得懂嘛 , 我们要想听懂 , 也得先复习一下高斯的想法 。
- |莫湾基场口一直都是非常热受争议的场口,盛产乌黑颜色的翡翠原石
- 基层|阳东启动送春联进万家活动
- 王志安&他的楷书很轻盈,以褚楷为基,兼收行意,洒脱清丽,严谨中蕴灵动
- 刘勤兵@新春走基层丨艺术让布依村落“靓起来”
- 虎舞@新春走基层 | 在海口跟着非遗过大年
- 姚叶红#本土艺术家组团慰问基层民警,饱蘸浓墨讴歌警民鱼水情
- 罗斯基勒·峡湾的夏日&丹麦不止有艺术大师哈默修依,画家LA Ring开创了象征主义的绘画
- 新闻记者$【新春走基层】聊城茌平:小朋友制作“虎宝宝”花糕迎新年
- 文化|踏雪冬捕 游人纳福
- 环保$济宁一地上榜第二批省级环保科普基地名单
