在平面上 , 我们知道如何测量一段直线的距离 , 用公式表示就是:
ds2 = dx2 + dy2
其实就是欧几里得几何中的勾股定理 。
那么在曲面上的弧长公式呢 , 高斯给出了公式:
ds2 = E du2 + 2F dudv+ G dv2
E、F、G都是系数 , 和曲面上点的性质有关 , u就是横坐标 , v就是纵坐标 。
要是在平面上 , 这个公式就可以又变回了勾股定理 , 还是ds2 = dx2 + dy2
高斯所说的这一切都还在二维平面中 , 黎曼把高斯的二维平面扩展到了n维平面 , 黎曼称之为黎曼流形 , 还用黎曼度规表达出来了高斯弧长公式中的E、F、G

文章图片
不难看出这就是高斯弧长公式在n维流形中的表达式 , 其中gij(p)就是p点的黎曼度规 , 黎曼度规随p的变化而变化 , 这种随空间的点变化的物理量是什么呀?当然就是场 。 在法拉第1837年提出电场磁场的概念17年后 , 黎曼给出了场的数学描述 。
用黎曼度规表示后 , 弧长公式就变成了这样 。
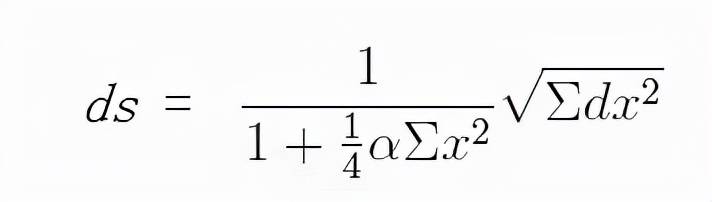
文章图片
文章图片
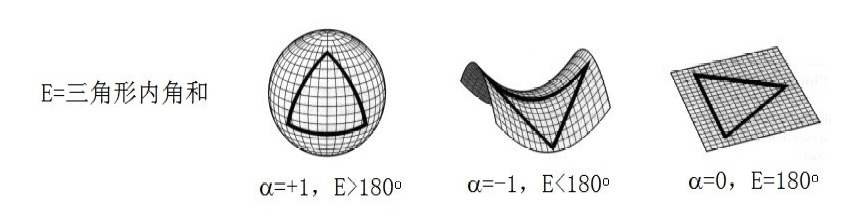
式中的α就是是二维曲面的高斯曲率 。
当α=-1 , 三角形的内角和小于180o , 这就是罗巴切夫斯基的双曲几何 。
当α=0 , 三角形的内角和等于180° , 这就是通常的欧几里得平面几何 。
当α=1 , 三角形内角和大于180° , 这就是球面几何 。
如果说罗巴切夫斯基的非欧几何撕开了欧几里得几何的一个角的话 , 黎曼几何就完全颠覆了欧几里得 。
现在可以看出来吧 , 欧几里得几何就是黎曼几何的一种特殊形式 , 只是在二维的小空间内适用 , 这句话是不是听起来有点熟悉呀?好像物理上也有这句话 , 物理上是这么说的 , 牛顿力学只是相对论力学在低速宏观情况下的近似 , 这么看来 , 黎曼几何是不是和相对论有关系呢?当然有关系 , 要是没有黎曼几何的话 , 也就没有相对论了 。
- “懒家伙”爱因斯坦
说这句话的人是爱因斯坦的老师闵可夫斯基 。 这个名字听起来好像是罗巴切夫斯基的老乡 , 其实他是正宗的德国人 , 和俄国也算有点关系 , 他出生在俄罗斯 , 他是希尔伯特的好友 , 希尔伯特在1900年的那场著名的关于数学的演讲就是出于他的建议 , 他还有一个身份就是爱因斯坦的大学老师 。

文章图片
现在人们都知道了爱因斯坦小时候做小椅子的传说是假的了 , 而且爱因斯坦从小到大都是老师们青睐的好学生 , 可闵可夫斯基怎么就看他不顺眼呢 。
这是由于爱因斯坦经常逃他的数学课 , 爱因斯坦逃课当然不是因为老师讲的不好 , 这一方面是爱神觉得物理用不了那么多数学 , 浅尝即止就可以了 , 另一方面是爱神有一个好老婆和一根好基友 , 好老婆是米列娃 , 好基友是格林斯曼 , 这俩都是学霸 , 平时爱神看看老婆和基友的笔记也就能混个及格了 , 至于上不上课倒是没多大必要 。
可是爱因斯坦真的错了 。

- |莫湾基场口一直都是非常热受争议的场口,盛产乌黑颜色的翡翠原石
- 基层|阳东启动送春联进万家活动
- 王志安&他的楷书很轻盈,以褚楷为基,兼收行意,洒脱清丽,严谨中蕴灵动
- 刘勤兵@新春走基层丨艺术让布依村落“靓起来”
- 虎舞@新春走基层 | 在海口跟着非遗过大年
- 姚叶红#本土艺术家组团慰问基层民警,饱蘸浓墨讴歌警民鱼水情
- 罗斯基勒·峡湾的夏日&丹麦不止有艺术大师哈默修依,画家LA Ring开创了象征主义的绘画
- 新闻记者$【新春走基层】聊城茌平:小朋友制作“虎宝宝”花糕迎新年
- 文化|踏雪冬捕 游人纳福
- 环保$济宁一地上榜第二批省级环保科普基地名单
